高考中的几何分布概率秘籍：解锁高分新技能

一、几何分布的定义与性质

定义：几何分布是一种离散型概率分布，描述了在n次伯努利试验中，第k次试验刚好获得第一次成功的机率。这里的伯努利试验指的是每次试验只有两种可能的结果：成功和失败，并且每次试验的结果都是独立的。性质：如果随机变量X表示在伯努利试验中获得首次成功的试验次数，且每次试验成功的概率为p（0<p<1），那么几何分布的概率质量函数可以表示为P(X=k)=(1-p)^(k-1)×p，其中k=1,2,3,...。几何分布的期望E(X)=1/p，方差D(X)=(1-p)/p²。

二、几何分布在高考中的应用

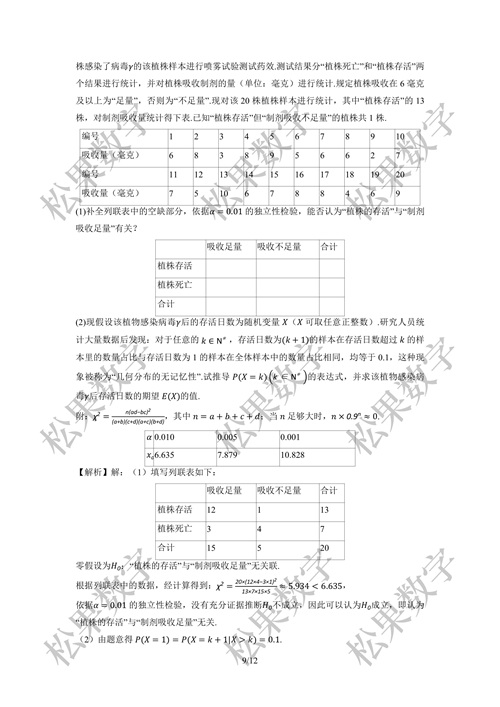
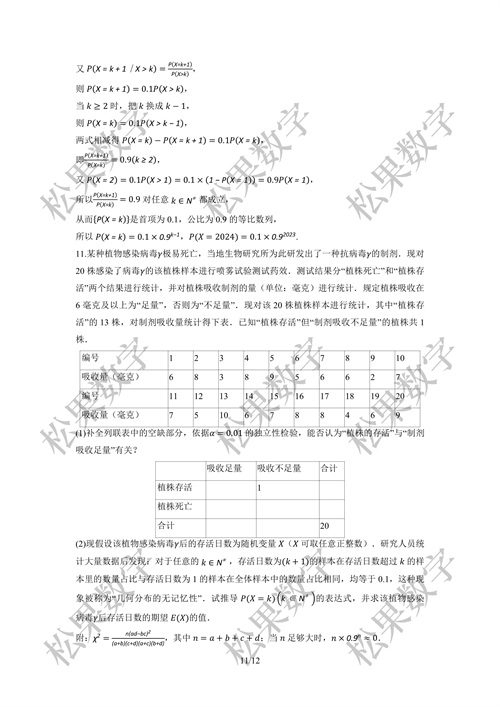
实际问题建模：在高考中，几何分布常被用于解决实际问题，如某种产品的寿命、某种疾病的传染率、篮球比赛中的角球投掷成功率、血液学中的验血试验次数等。这些问题都可以通过几何分布进行建模和求解。典型题型：高考中常见的几何分布题型包括计算某事件首次发生所需的试验次数、给定试验次数下事件发生的概率等。这些题型要求学生能够熟练掌握几何分布的概率质量函数，并能够根据实际问题进行灵活应用。解题技巧：在解决几何分布问题时，首先要明确问题的背景和条件，确定每次试验成功的概率p。然后根据几何分布的概率质量函数P(X=k)=(1-p)^(k-1)×p，将实际问题转化为数学表达式。最后通过计算求解出所需的结果。

三、高考备考建议

理解概念：深入理解几何分布的概念和性质，掌握其概率质量函数和期望、方差的计算方法。多做练习：通过多做高考真题和模拟题，熟悉几何分布在高考中的题型和解题技巧。注重应用：将几何分布与实际问题相结合，提高解决实际问题的能力。

综上所述，几何分布在高考中具有重要的应用价值，通过深入理解和掌握其概念、性质以及解题技巧，可以有效地提高高考数学成绩。

免费资料可点击：教研平台